Croquet is a Game
Probabilities, Statistics and Such
The game of croquet is not a game of perfect -- but it is close to
being one. Like golf, the game involves mechanical motions which
start and end with the balls at rest. Thus, unlike tennis or
badmitten there is no need to estimate the speed or spin of a ball
arriving from your opponent. Like a game of chess, the moves can
be planned ahead and when executed properly can lead you to making an
all around break. How and where you leave the balls for your
opponent may give you the best chance of either keeping the inning
(i.e. control of the game and ability to make more hoops) or of losing
the inning resulting in a turnaround to your opponent.
At all levels of the game, the risks and rewards of your plans and
executions lead to the ultimate outcome of either a win or loss.
[This is a work in progress]
Let me illustrate a few principles of probabilities and how exact a
player in this sport needs to be.
Probability of Winning a Best of Five
or Three
Match
When playing a single game against an opponent, the probability of
winning may be equal to 'p' which is a number between 0 and 1
representing the percentage of games that would be won by that
particular player against that particular opponent. The
opponent's chance of winning is denoted at 'q' and is equal to '1-p'.
A number of 0.5 represents an equally likely chance to win or loss,
otherwise known as a 50/50 chance or 1:1 odds. When more than
0.5, the player has a better than even chance of winning. 0.7 for
example would be 7:3 or better than 2:1 odds.
If a player plays in a best of three (or best of five) match, then the
odds of winning the match change.
The better player has a better chance of winning that match. Here
is a graphical picture of how the odds change.
The straight line represents the chance of winning one game. The
line the middle is the chance of winning a Best of Three match and the
most curved line represents the chance of winning a Best of Five match.

Here is a table of these probabilites
...
single game best of 3 best
of 5
0.0500000 0.0072500
0.0011581
0.1000000 0.0280000
0.0085600
0.1500000 0.0607500
0.0266119
0.2000000 0.1040000
0.0579200
0.2500000 0.1562500
0.1035156
0.3000000 0.2160000
0.1630800
0.3500000 0.2817500
0.2351694
0.4000000 0.3520000
0.3174400
0.4500000 0.4252500
0.4068731
0.5000000 0.5000000
0.5000000
0.5500000 0.5747500
0.5931269
0.6000000 0.6480000
0.6825600
0.6500000 0.7182500
0.7648306
0.7000000 0.7840000
0.8369200
0.7500000 0.8437500
0.8964844
0.8000000 0.8960000
0.9420800
0.8500000 0.9392500
0.9733881
0.9000000 0.9720000
0.9914400
0.9500000 0.9927500
0.9988419
1.0000000 1.0000000
1.0000000
Exactly how good are good croquet
players ??
Well think of this .... if a player runs an all
around 4-ball break, he
must hit each ball once, taking croquet from each ball and then running
the hoop. One must do this for
12 hoops without failing any particular shot. In a perfect all
round break there would be 84 strokes executed flawlessly. If a
player is able to do this most of the time, i.e. better than 50% of the
time, then the probability of each stroke must be better than
99%! In fact, he must not miss more than 82 shots out of 10,000.
And if you are one of those players than can make
two all around
flawless breaks and peg out to win, then you must play 175
strokes flawlessly. You better not miss more than 39 shots in
10,000
strokes. Each shot should come off with an average success rate
of 99.605%.
If you need to do this say 10 games in a row to win
a tournament, then
one would need to miss less than 4 shots in 10,000 strokes.
Many of the top players (perhaps the top 100 in
the world) manage to do
this while peeling their opponent through their last 3, 4 or even 6
hoops. For these players, like Stephen Mulliner as an
example, find the aspect of peeling very appealing because it helps
them
maintain their focus on the game, the need for flawless stroke
execution which prevents the mind from wandering off to other mundane
things.
As a practical note, not every stroke has an
equally likely probability
of success. In a given all around break, usually there are 1 or 2
'questionable' strokes near the beginning of the break that tend to
'make it work'. These strokes are the necessary ones to do to
either build the break by picking up a ball that is out of position or
a difficult stroke is required to make an angled hoop shot to continue
the break. The
overall probability of success of any sequence of events is always less
than the probability of success of any given shot. The
chain of
events in a perfect round require a progressive multiplication of
probabilites.
To give a specific example, let's say that two
strokes have a
probability of success of 80% and the other eight strokes have a
probability of
sucess of 99.9%, then the overall probably of success of all 10 strokes
is equal to 'xyz'.
xyz = 0.8 * 0.8 * 0.98^8 = .8 * .8 * .851 = 0.544 or
54.4% chance of success
Thus to complete two successfully flawless breaks
(50% of the times)
as previously mentioned with two shots of 80% probability, then the
probability of success of the remaining shots must all be better than
99.857% or less than 14 errors in 10,000 shots.
Anyway you look at it, there is little room for
sloppiness!
World Rankings
The players of Association croquet are tracked in a database maintained
by Chris
Williams and known as the World Rankings. These players have
played in a variety of croquet events from local club tournaments to
national and world tournaments. Many have traveled around the
world and thus the rankings are a fair collection of all the
individuals in the sport and once a player has played in a dozen or so
events, the player's ranking becomes a bit better defined.
Initially it seeks a seemingly random value but eventually it
settles(?)
to a fairly constant one.
When players improve and win more games from more experienced players
(with higher Index points) they collect more Index points than they
give away. Index points are shared between players and when a
player with less Index points defeats an opponent with more Index
points, then the winning player collects proportionately more points
than he would collect if he had defeated a weaker opponent (with less
Index points). This is done using an agreed upon mathematical
formula.
The Grade changes more slowly than the Index because it is a running
average of the Index points. A simple first order digital filter is
used to compute the Grade. Improving players are usually judged
by when their Index is greater than their Grade because this means that
the Grade will continue to increase as long as this is true. This
system is slightly flawed because the filter is not capable of
rejecting the random noise present in this fundamental stochastic
process. Winning and losing are part of the battle and the Index
points jump and down randomly as games are won and lost.
For more information about World Rankings, go to the source ... World
Croquet
Rankings and Chris
William's Website
The World Rankings might provide a means for
judging the probability against any two given players.
One player ranked with an index of 2000 should be capable of running
two all around breaks while triple peeling his partner.
While this is an agreed upon standard there are some players as low as
1500 with triple peels and some with Grades as high as 2300 without
peels.
And if a players can triple peel out his partner, then he removes the
potential need for his opponent to miss the 2nd lift shot. The
opponent that can triple peel against an opponent that does not triple
peel is likely to win 2:1 more games if it comes down to hitting in
long shots and running around a break. Thus I roughly estimate
that the odds of winning for a player with a ranking of 2000 against a
player with a ranking of say 1800 is roughly 2:1 or a probabilty chance
of 0.66. A good handicapper likely studies the results and can
estimate the odds between two players with two different rankings.
In fact, Louis Nel worked out from the mathematical equation that is
used to exchange Index points between the winning and losing players a
table showing the probabilities versus the difference between the two
players Index (or Grade I presume).
Here
is a percentage table which was calculated by Louis Nel.
Here
is a good explanation by Louis Nel of how the Index points are
calculated.
Here is a
explanation by Louis Nel as to random fluctuations of World Rankings.
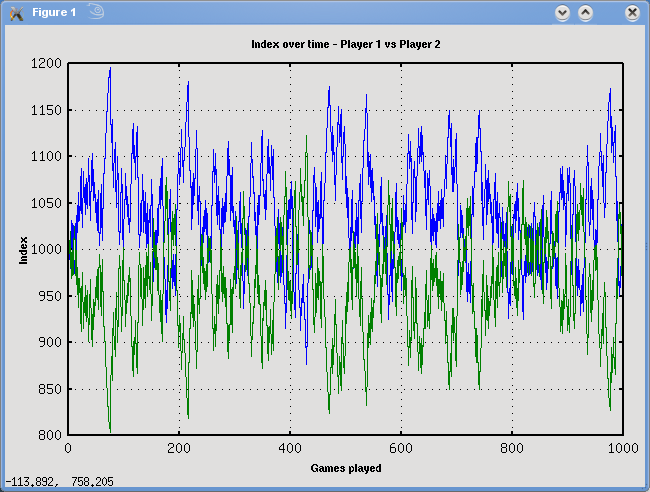
To illustrate how the Index changes between two players, I setup a
random experiment between the Player 1 with a winning chance of 60%
against Player 2. Then, an experiment of 1000 games was conducted and
the resulting graph shows their Index as it changes over time. As
can be seen sometimes the Indexes overlap. On
average, the Index of Player 1 is 1040 and Index of Player 2 is 960.
The Grade is a smoothed representation of the Index as it changes in
the previous experiment. Several key things to note is that the
Grade changes by 200 points from a low of 940 to a high of 1140
The Grade takes about 50 games to settle(?) to 1050. Each random
experiment produced different but similar results. The average
difference between these two players Grades agrees with Louis Nel's
predictions. The practical use of these tables to predict the
outcome of any particular event is a bit dubious.
The game is partly a game of chance but mostly of skill (see Exactly
How Good are Croquet Players?) which means that the outcome of any
single game or match is not known with any certainty but those players
with high rankings have lots of experience, confidence and a chance of
winning. The most important thing is that given a chance to play
a stronger player, you should ALWAYS take the opportunity because you
are more often then not likely to learn something new which will help
you improve your ranking and experience level.
Rankings continue to change as players continue to play, learn and
grow. In fact, the greatest problem in predicting the outcome of
a particular game, match or tournament is the fact that any players
true performance index is rarely accurately reflected with a single
number no matter how recently the indexes were created. Certain
players seem to have the strategic and psychological advantage over
some players, maybe due to particular techniques or styles which play
in certain ways against/for the various players.
This is all why we play the game and enjoy it at all levels. The
outcome is never certain until just after the pegout and the game is
over.
[maybe Chris Clarke can share some table of odds versus grade index ...]
Ladder Playoff Formats - Ladder vs
Round Robin
The format of play during tournaments is always an interesting topic
amongst the players. Some tournament directors are more
formalized in their seeding and playoff ladders while others sometime
appear to follow random, strange or incorrect methods. Whatever
you face when you play in a tournament, you are most likely at the
mercy of your tournament director as they ultimately have the final
authority as to how to organize the playoffs that determine the final
winner. The most important thing is to remain calm, ask questions
and go along with the decisions that are made by your tournament
director.
The best organized tournaments are organized and documented well in
terms of who plays who, when and on what day, what factors will
determine the winner and the players with the best records, what
happens if players withdraw, and any special conditions of the
tournament play. Tournaments are organized with a variety of
formats which should be described in the tournament annoucement or when
requested by players prior to entry (and definitely in the players
booklet prior to the start of the event).
A very good explanation of Round Robin and other tournament formats is
contained in Wikipedia. Check out this link.
The disadvantage of using any single standard format is that each
format has its pros and cons. Many of the major tournaments in
the US attract players from all across the country and one of the
greatest arguments against a single elimination ladder tournament is
that half of the players are eliminated from the tournament after the
first round of play. Even in a best of three match, this may mean
that you travel across the country to play two games. An
expensive way to spend $1000, with few if any tournaments offering
winning purses enough to offset travel and accommodation expenses.
On the other hand, a round robin format (where every player plays each
other) does not always produce a clear cut winner. Sometimes net
or gross points are used to 'settle' the question of the outcome, and
other times head-to-head determinations are made, but in all of these
cases, when the winner is not clearly decided on the basis of net wins,
then the outcome of the tournament is not cleanly decided.
A popular format pioneered by croquet player Stan Patmor was to combine
the idea of a round robin format at the beginning of a tournament
followed by a playoff ladder. Players are grouped into blocks (or
what in is known as divisions in baseball). Players advance or
qualify to the ladder playoff based upon their results in their
division or round
robin block play. All players are guaranteed a set number of
games (usually equal) (in the round robin) and the tournament playoff
ladder brings the best
players together at the end for a Final match. This format is
called the Patmor draw.
Another format for tourmament play is called the Swiss and is very
popular for Chess tournaments where players of varying abilities and
numbers play. It has many advantages over either ladder or round
robin play but is more difficult to manage since it requires the
tournament director to select the appropriate player matchups after
each playing round. The advantage is that it can guarantee every
player a set number of games and during the course of the event,
players 'migrate' toward players of equal playing performance.
Any number of rounds equal to or greater than that required for ladder
playoff may be used. The more the better and probably an odd
number is best.
Many criticize the block player round robin format because it does not
clearly delineate winners from losers, but in reality unless many games
(i.e. rounds) are played between two opponents (and in a tournament
between a great variety of players), the outcome of any tournament has
several opportunities for choosing a particular winner. This is
often tried to be addressed by 'seeding' the various parts of the draw,
but this too is likely to yield opportunities for inequities and
perhaps unfair advantages to some if not all of the better
players. It all comes back to probabilities and if a particular
opponent has a 60% chance of winning then he or she also has a 40%
chance of losing.
When a block of players end playing a round robin event and three end
up tied for 1st place and 2 tied for 4th place and the rest tied for
6th place, then all that has been determined is that there are 3
players that likely are about equal in ability followed by 2 others
followed by the other 3 players, but even this is not really sorted
out. Maybe the player that finished 5th is actually the strongest
player. After all, an outcome of chance might still allow this
result to occur.
And is a ladder playoff, while always clearly leading to a given
winner, more likely or less likely to produce a result with the
strongest player as the winner? [a good question of probabilities --
Louis Nel may have the answer, he has shown some results of a ladder
playoff which uses a random draw versus a seeded draw, but has he
compared these to the results against a round robin type of draw.]
My feeling is that the Swiss type of draw is the best format and should
be used more often in the determination of main croquet events (it is
often used but more often improperly applied in consolation plate
events).
The seeding and draw process used in the WCF championships after the
qualifying block round robin play is quite interesting. It makes
for a good discussion at a cocktail party or on the Nottinghma forum.
My argument is simply that if a block play (round robin event) results
without a clear cut winner, then maybe that is because there is no
clear cut winner, maybe two or three folks are really close to playing
grade. A ladder (knockout) round will definitely NOT show
that type of result. I've advanced through to the end of a ladder
knockout having played less than 1/4 of the field. I hate going
to a what would otherwise be a great tournament but end up leaving
after having played only a few of the players.